[백준/Java] Fly me to the Alpha Centauri
문제

입력
입력의 첫 줄에는 테스트케이스의 개수 T가 주어진다. 각각의 테스트 케이스에 대해 현재 위치 x 와 목표 위치 y 가 정수로 주어지며, x는 항상 y보다 작은 값을 갖는다. (0 ≤ x < y < 231)
출력
각 테스트 케이스에 대해 x지점으로부터 y지점까지 정확히 도달하는데 필요한 최소한의 공간이동 장치 작동 횟수를 출력한다.
내 풀이
dist = y - x 로, 거리를 나타낸다고 할 때, 해당 거리까지 이동할 때의 max 값은 거리(dist)의 제곱근을 구함으로써 알 수 있습니다.
거리 = 5일 때, 제곱근을 구하면 2.x가 나오고, 정수형으로 변환하여 2라는 max 값을 얻을 수 있습니다.
다음은 거리 1부터 16까지 작성한 표입니다. 주황색 부분은 제곱수를 표시했습니다.
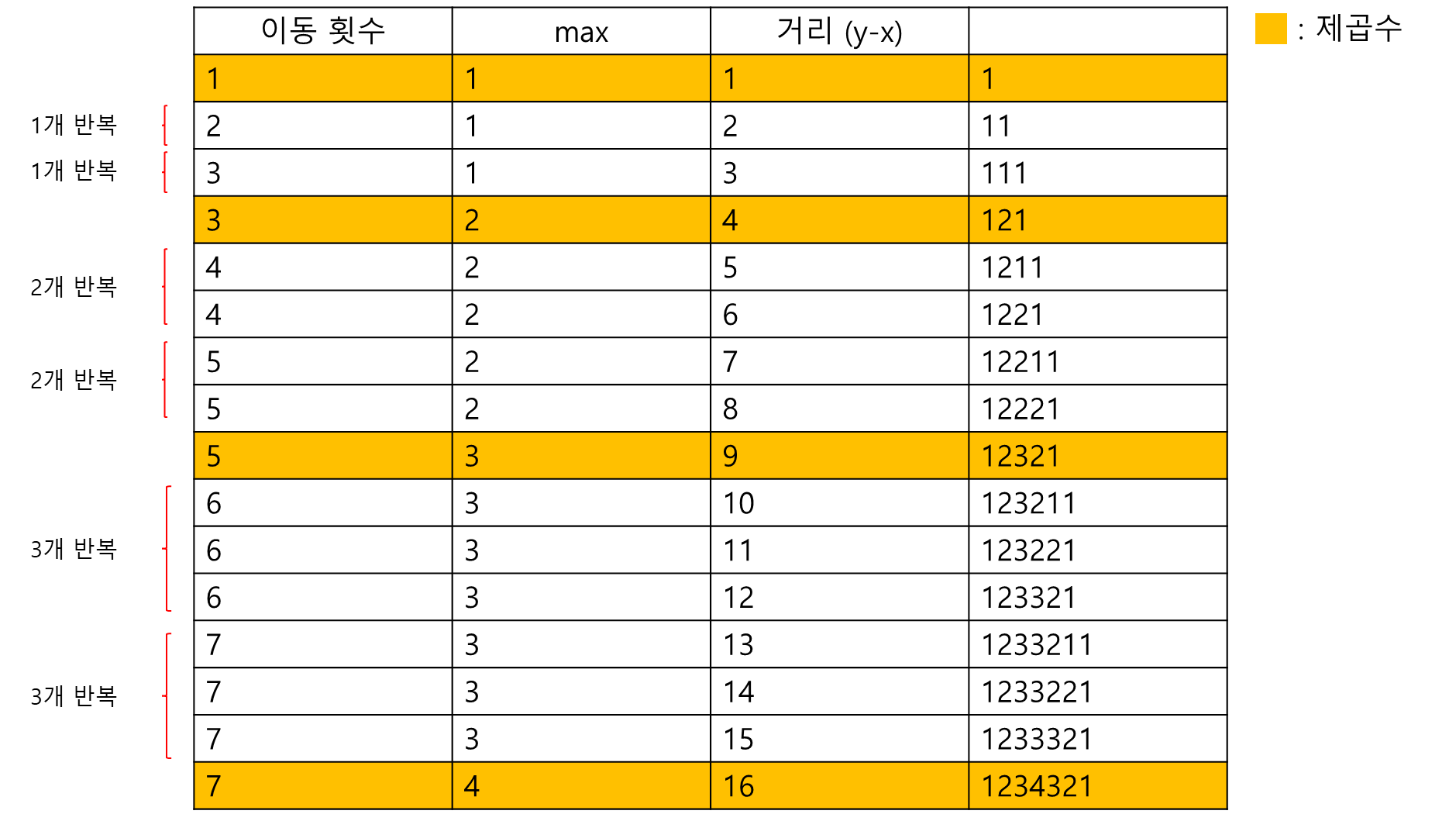
제곱수부터 다음 제곱수 전까지는 같은 max값을 가집니다.
제곱수가 아닌 수는, max 값을 제곱한다고 해서 실제 거리와 같아지지는 않습니다. max를 구할 때 제곱근에서 소수점을 버렸기 때문입니다. 때문에 거리가 제곱수인 경우와 아닌 경우를 나누어 계산해주어야 합니다.
ex) 거리 = 4, 제곱근 = 2, max = 2, max^2 = 4
거리 = 5, 제곱근 = 2.xx, max = 2, max^2 = 4
거리 = 6 제곱근 = 2.xx, max = 2, max^2 = 4
여기서 max의 제곱이 거리와 같은 경우 (거리가 제곱수인 경우), 이동횟수는 2*max+1 임을 구할 수 있습니다.
거리가 제곱수가 아닌 경우, 거리 5 ~ 8, 거리 10 ~ 15 와 같은 경우를 살펴봅시다.
제곱수 4부터 제곱수 9까지 거리가 5 ~ 8일 때, 제곱수 9부터 제곱수 16까지 거리가 6 ~ 15 일 때를 보면 규칙을 찾아볼 수 있습니다. 바로 제곱수 이후부터 max 값 만큼 이동횟수가 반복된다는 것이죠.
제곱수가 아닌 경우, 제곱수 기준으로 max개 까지는 같은 이동횟수, 그 이후로 max개가 같은 이동횟수를 갖는 것입니다.
그렇다면 거리가 (제곱수 + max) 보다 큰지 작은지를 판단하면 됩니다. 제곱수는 구해두었던 max로 계산해줍니다.
수식을 구하면 dist < max * max + max 인 경우 이동횟수는 2*max+1 이고, 작거나 같은 경우는 2*max 임을 구할 수 있습니다.
import java.io.*;
import java.util.*;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int size = Integer.parseInt(br.readLine());
for (int i = 0; i < size; i++) {
StringTokenizer tk = new StringTokenizer(br.readLine());
int x = Integer.parseInt(tk.nextToken());
int y = Integer.parseInt(tk.nextToken());
int dist = y - x;
int max = (int) Math.sqrt(dist); //정수
if (max == Math.sqrt(dist)) {
bw.write(2 * max - 1 + "\n");
} else {
if (dist > max * max + max) bw.write((2 * max + 1) + "\n");
else bw.write((2 * max) +"\n");
}
}
bw.flush();
bw.close();
br.close();
}
}